|
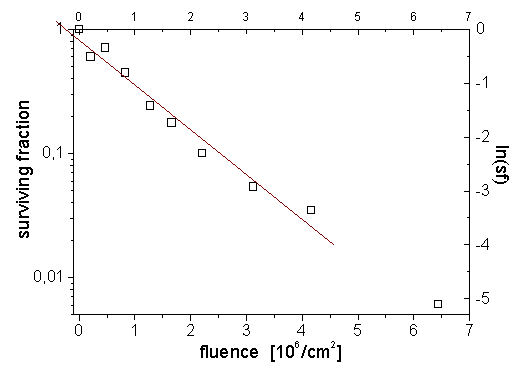
Abb. _01: Die Häufigkeit des Treffens des Zellkerns durch 218Pb-Alpha-Teilchen in Abhängigkeit von der Dosis: über der durchschnittlichen pro Zelle applizierten Alpha-Energiedosis ist in der unteren Hälfte des Graphs für den niedrigen Dosisbereich der Anteil der getroffenen Zellkerne (rechte Achse) sowie die lokal in diesen Zellkernen abgegebene Dosis (linke Achse) aufgetragen. Im oberen Teil ist für den hohen Dosisbereich, wo jede Zelle durchschnittlich mindestens einmal getroffen wird, die mittlere Zahl der Treffer pro Zellkern aufgetragen. Hier wurde von einem Zellkerndurchmesser von 8 µm ausgegangen, wie man ihn in Säugetierzellen findet. [Feinendegen, 1978, nach Burkhart, 1991].
|
BESONDERHEITEN DER BIOLOGISCHEN WIRKUNG VON STRAHLUNG
|
|
||||||||||||||||
 |
||||||||||||||||||
| Ionisierende Strahlung und UV-Licht schädigen die einzelnen Körperzellen besonders effektiv, weil sie selektiv die in ihnen enthaltene Erbinformation, die alle Lebensabläufe steuert, (das Genom) zerstören oder verändern. Aufgrund dieser genotoxischen Wirkung der Strahlung reicht die Energie einer Tasse warmen Tees - in Form von Röntgenstrahlung verabreicht - aus, um einen Menschen zu töten. In einigen Punkten unterscheidet sich die Wirkung von Strahlung jedoch sehr von der anderer genotoxischer Substanzen. Im Gegensatz zu den meisten anderen chemischen oder physikalischen Noxen, die auf biologische Zellen einwirken können, ist die Energiedeposition durch Strahlung in ihrer zeitlichen und örtlichen Ausdehnung sehr komprimiert. Eine genotoxische Chemikalie wie z.B. Aflatoxin B, die selbst in der sehr geringen Konzentration von 1 µg pro kg (1ppb) noch wirksam ist, liegt dann bei angenommener homogener Verteilung immer noch in einer Konzentration von 10.000 Molekülen pro Zellkern vor. Eine Dosis 60Co-g -Strahlung von vergleichbarer akuter genotoxischer Wirkung, nämlich 0,3 mGy, würde für jeden Zellkern eine Wahrscheinlichkeit von 10% bedeuten, von einem Elektron getroffen zu werden. Bei einer gleichartigen Dosis Teilchen-Strahlung wäre die Wahrscheinlichkeit der einzelnen Zellkerne, von einem Elektron getroffen zu werden, noch deutlich geringer. Da weiterhin gilt, daß strahleninduzierte Radikale nach ihrer Entstehung maximal einige Nanometer zurücklegen können, zeigt dies, daß Strahlung in den einzelnen getroffenen Zellen bzw. Zellkernen immer zumindest eine gewisse Minimaldosis appliziert, die im Vergleich zu der über das ganze bestrahlte Gewebe gemittelten Dosis sehr hoch ist. Die Wahrscheinlichkeit für jede individuelle Zelle, getroffen zu werden, ist also sehr gering; wird sie aber getroffen, so ist die erhaltene Dosis hoch (in Abb. _01 am Beispiel von a -Strahlung gezeigt). Dieses Verhalten ist bei Teilchen-Strahlung, vor allem im aus Strahlenschutzgründen besonders interessanten Niedrig-Energie-Bereich stark ausgeprägt. [Burkhart, 1991]
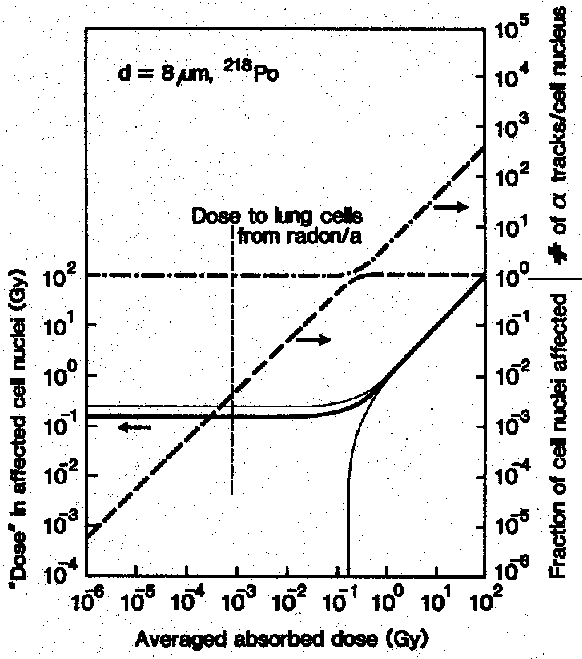
Abb. _02: Beispiel einer Überlebenskurve, d.h. der Dosis-Effekt-Kurve, die die Zahl der teilungsfähig gebliebenen Zellen mit der erhaltenen Strahlendosis korreliert. Die Zahl der überlebenden Zellen nimmt in erster Näherung exponentiell mit der Dosis ab. Um eventuelle Unterschiede im Verlauf der Überlebenskurven besser sichtbar zu machen, wählt man daher meist eine halblogarithmische Darstellung.(Hier V79-Zellüberleben nach 9,3 MeV/u-Xenon-Bestrahlung.) Die Inaktivierung von Zellen durch Strahlung ist stochastischer Natur und folgt daher statistischen Gesetzmäßigkeiten. Dies liegt an der Zufälligkeit des Treffens (bzw. Nicht-Treffens) essentieller DNA-Bereiche durch die einzelnen Elektronen oder Teilchen. Daher kann das Zellüberleben nach Strahlung durch die Poissonverteilung beschrieben werden, wodurch auch der exponentielle Verlauf der Überlebenskurven begründet ist (Abb _02). Dabei ist P(X=j) die Wahrscheinlichkeit, daß j Zellen überleben. Wenn die ursprüngliche Anzahl ausgeplatteter Zellen pro Platte n, und die Wahrscheinlichkeit des Zellüberlebens pn ist, so ergibt sich P(X=j) zu: Tab. _01: Wahrscheinlichkeit für die Anzahl der überlebenden von 200 ausgeplatteten Zellen, bei einer tatsächlichen Überlebenswahrscheinlichkeit von 0,01 %:
Zu diesen unvermeidbaren Ungenauigkeiten kommen weitere, z.B. die der Zellkonzentration beim Pippettieren der Zellsuspensionen. Sie sind bei der Fehleranalyse zu beachten und auch beim Fitten einer Kurve an die Daten-Punkte. Beim Anfitten sollten die Daten in eine solche Form gebracht werden, daß der aus diesen Komponenten bestehende Fehler normalverteilt um die zu messenden Werte vorliegt. Kommentar: Dies ist ein Auszug aus Für Feedback bin ich ebenfalls dankbar. - Paul Schmidt |